递归总结

简介

递归：Recusion

Recusion is an approach to solve problems using a function that calls itself as a subroutine

函数结构

一般来讲，递归函数 = 终止条件（Base case） + 递归关系（Recusion relation）。

Base case：最小问题的解决方式
Recusion relation：大问题和小问题的关系

计算机的实现方法

1. 任何一个函数的调用，计算机会在内存中生成一块区域，用于存放函数的参数，返回的地址等，这块区域叫做「栈」。
2. 递归函数的调用会生成一系列的栈

递归一般有三种形式：

缓存（Memoization）

以经典的 斐波那契数列 为例

1. Base case：

$F(0) = 0;F(1) = 1$

2. Relation

$F(n) = F(n - 1) + F(n - 2)$

根据这两个条件很容易得出递归函数，而为什么需要引入缓存：

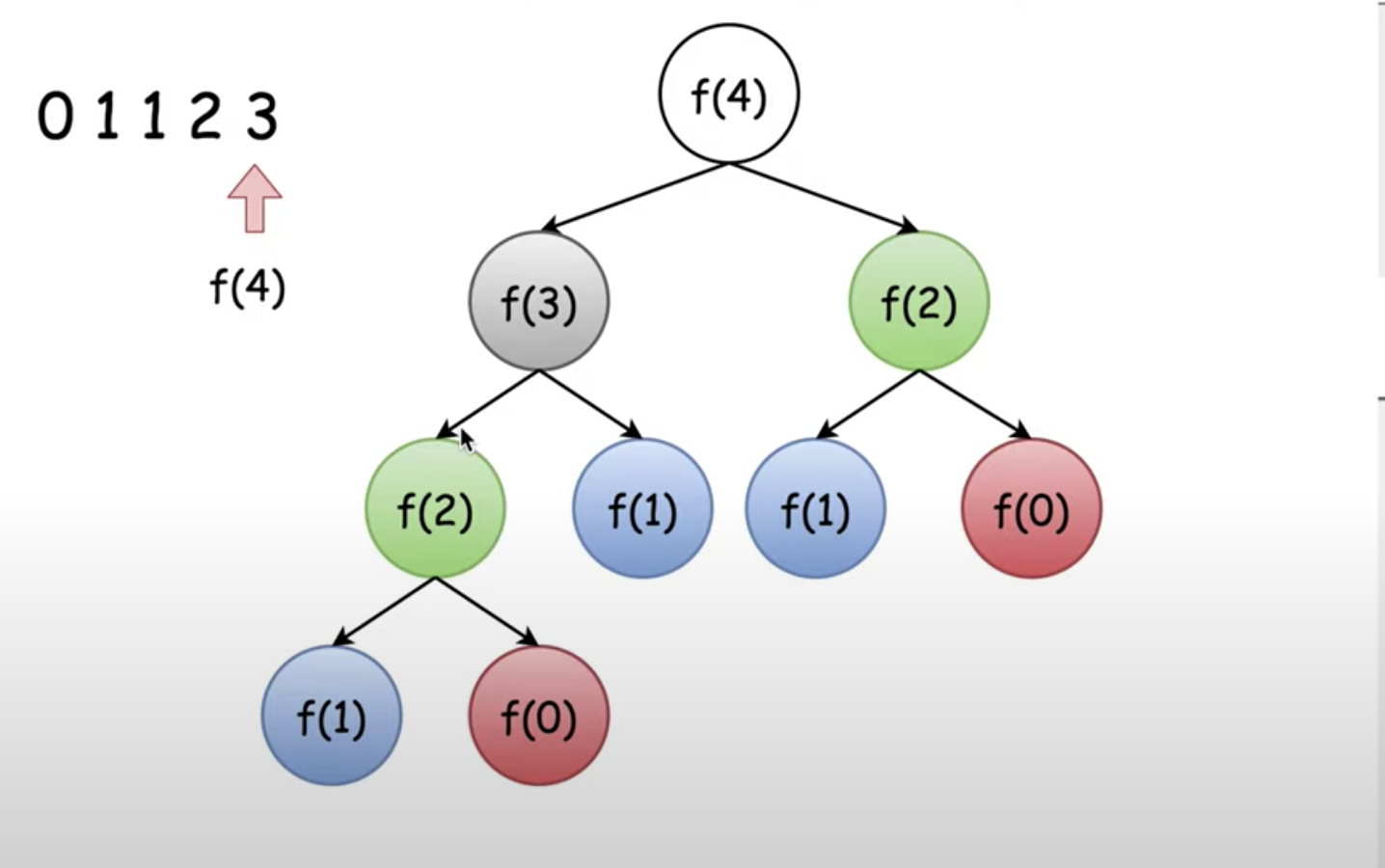
如上图：f(4) = f(3) + f(2)

而 f(3) = f(2) + f(1)

在计算 $f(3)$ 时，我们其实已经计算过 $f(2)$ 的结果，将 $f(2)$ 存入缓存则可以减少以空间换时间。

相关题目：

爬楼梯

分治（Divide and Conquer）

分而治之，几乎等同与标准的递归，唯一的区别是。最后需要将子问题的结果合并。

• Divide：将问题 $S$ 分解为子问题 {$S1$, $S2$, …$Sn$}
• Conquer：递归解决小问题
• Combine：合并每个结果

以 98. 验证二叉搜索树 为例

给定一个二叉树，判断其是否是一个有效的二叉搜索树。
一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

var isValidBST = function(root) {
    if (!root) {
        return true
    }
    function valid(root, low = -Infinity, high = Infinity) {
        if (!root) {
            return true
        }
        if (root.left && (root.left.val >= root.val) || root.val >= high ) {
            return false
        }
        if (root.right && (root.right.val <= root.val) || root.val <= low ) {
            return false
        } // base case

        return (valid(root.left, low, root.val) && valid(root.right, root.val, high)) 
    }

    return valid(root)
};

• base case: 如果左边的节点大于当前节点或者当前节点大于父节点，则为 fasle。右子树同理条件反之。
• 分治：将树 分解为左子树和右子树的校验的子问题
• 结合：将结果合并

将问题分解为：验证左子树 和 验证右子树。

分治模板

function divideAndConquer() {
    [S1, S2, ...Sn] = divide(S)
    rets = for (var i = 0; i < Things.length; i++) {
        divideAndConquer(Things[i])
    }
    [R1, R2, ...Rn] = rets
    return Combine([R1, R2, ...Rn])
}

回溯（Backtracking）

回溯问题的一般形式：寻找所有满足 XXX 条件的结果，并且问题可以递归实现。

以 LC22: 括号生成 为例

=======
Base case：

$F(0) = 0;F(1) = 1$

Relation

$F(n) = F(n - 1) + F(n - 2)$

根据这两个条件很容易得出递归函数

```js

为什么需要引入缓存：

st=>start: F(4)
op1=>operation: F(3)
op2=>operation: F(2)
op3=>operation: F(1)

st->op1->op2

分治（Divide and Conquer）

回溯（Backtracking）

LC22: 括号生成

/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function(n) {
    const result = []
    function backtracking(charactor = '', left = 0, right = 0) {
        if (charactor.length === 2 * n) {
            result.push(charactor)
        }
        if (left < n) {
            backtracking(charactor + '(', left + 1, right)
        }
        if (left > right) {
            backtracking(charactor + ')', left, right + 1)
        }
    }
    backtracking('', 0, 0)
    return result
};

• 使用两个 if 判断是否可以添加左右括号。不满足 if 的则为无效表达式
• 使用 charactor 表示当前变量。

回溯模板

function backtrack(candiate) {
    if findSolution(candiate) {
        outPut(candiate)
        return
    }
    for (nextCandidate in listOfCandiate) {
        if (is_validate(nextCandidate)) {
            place(nextCandidate)
            backtrack(nextCandidate)
            remove(nextCandidate)
        }
    }
}

相关习题：

• 98. 验证二叉搜索树
• 509. Fibonacci Number
• 22. 括号生成