不会快速幂的我留下了超时的悔恨泪水

快速幂算法简介

求 x^n 最简单的方法是通过循环将 n 个 x 乘起来，依次求 $x^1$, $x^2$, …, $x^{n-1}$, $x^n$ 时间复杂度为 O(n) 。

快速幂法可将时间复杂度降低至 O(log n) ，以下从「分治法」和「二进制」两个角度解析快速幂法。

二进制角度

利用十进制数字 n 的二进制表示，可对快速幂进行数学化解释

特殊情况：n 为 2 的幂，以 $a^64$ 为例：

其中 n = 64 为 2 的幂

朴素算法进行逐个相乘：$a * a … * a$ (时间复杂度为 O(n))

当 n 为 2 的幂时，我们只需 6 次乘法，时间复杂度为 O(log n)

n 不为 2 的幂，以 $a^{105}$ 为例：

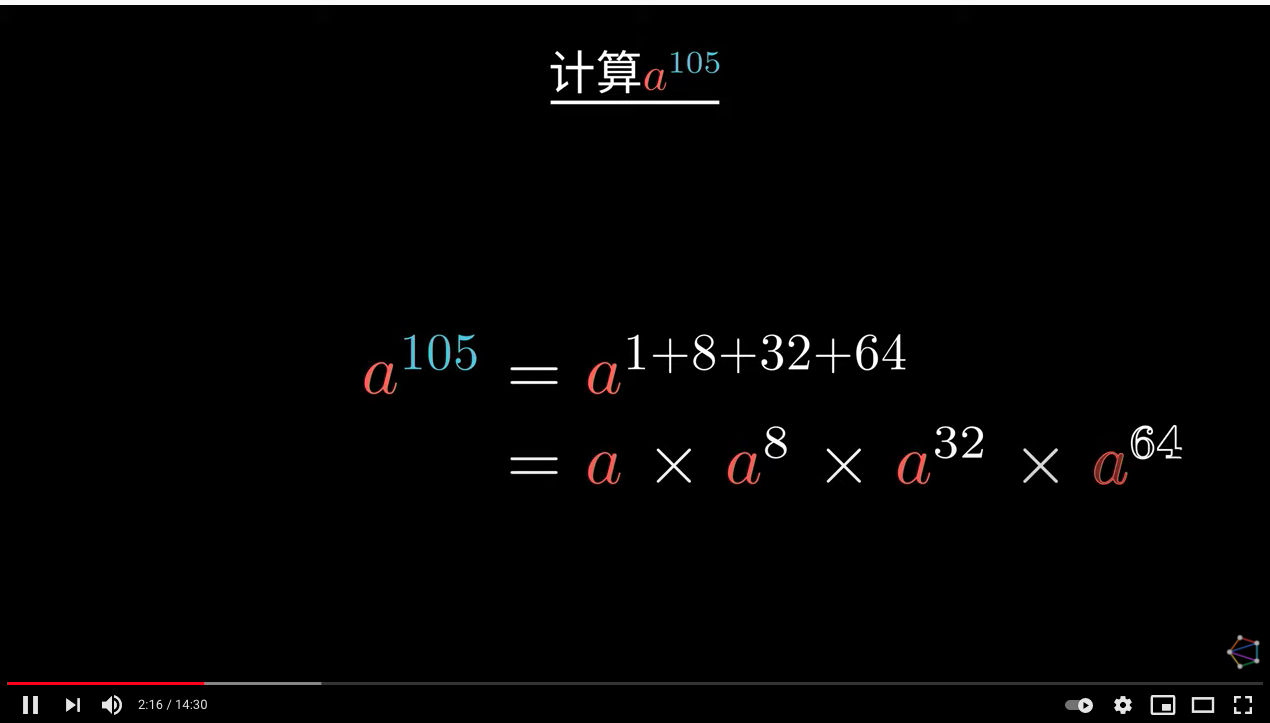
以上：计算 $a^1$，$a^8$，$a^{32}$，$a^{64}$ 是件容易的事，所以算法关键在于将 n 转化为 2 的幂之和

105 的二进制表示为：1101001，将这几个数字拆开刚好得到：$a^1$，$a^8$，$a^{32}$，$a^{64}$

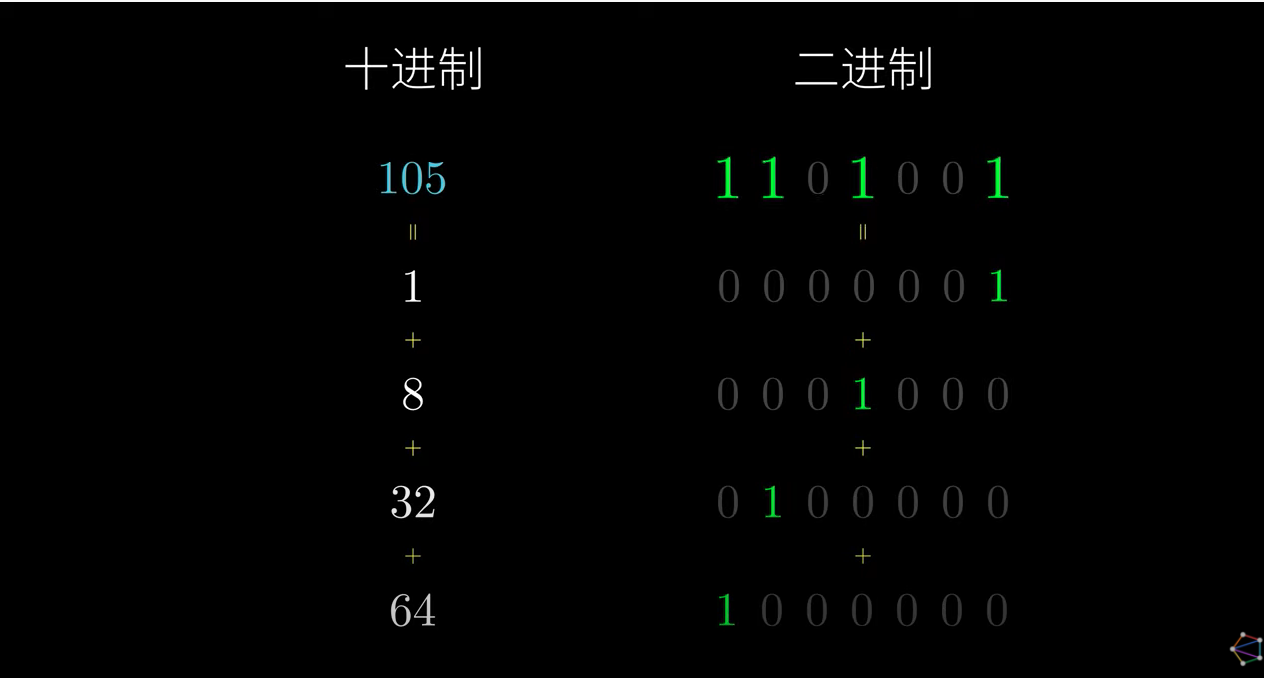
计算 $a^n$ mod m

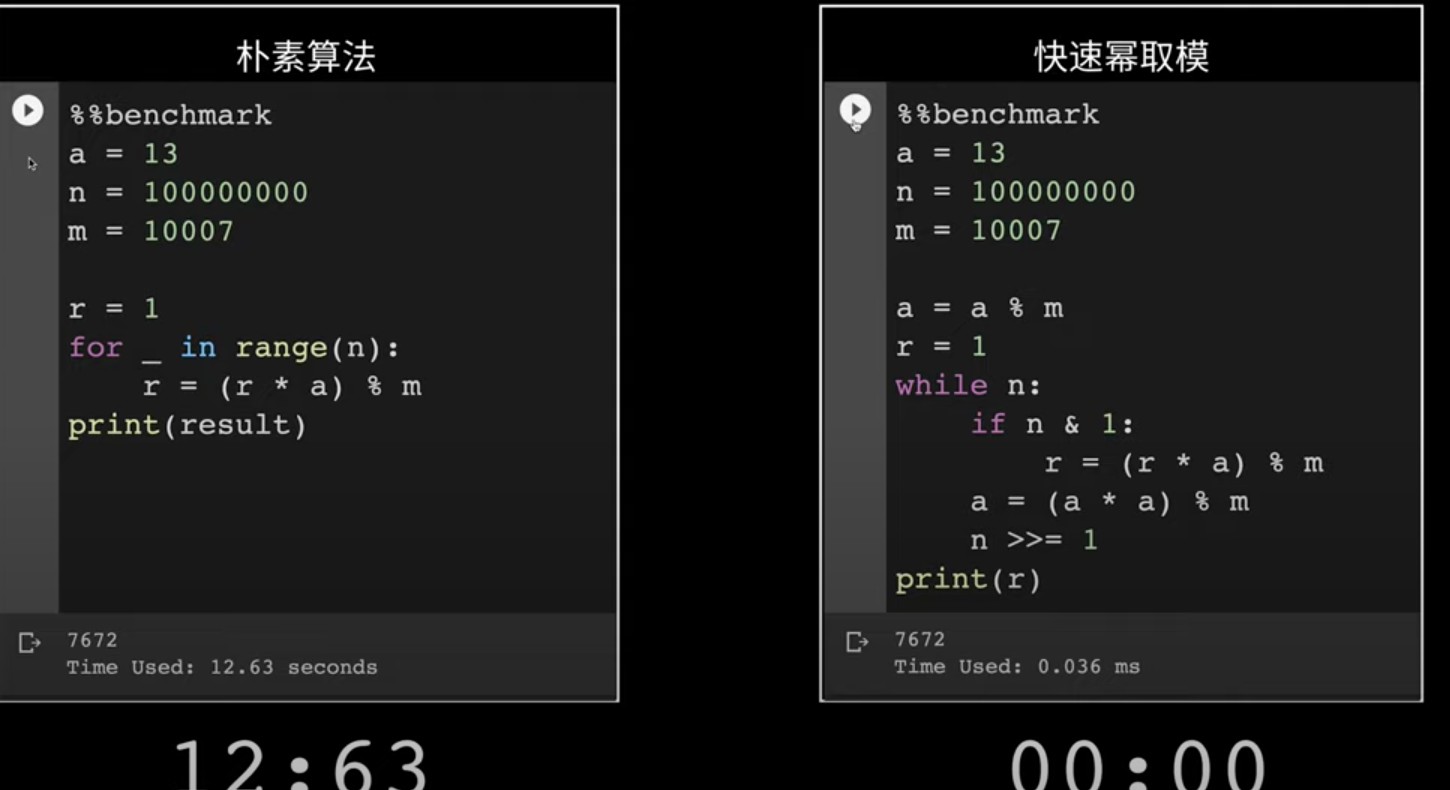
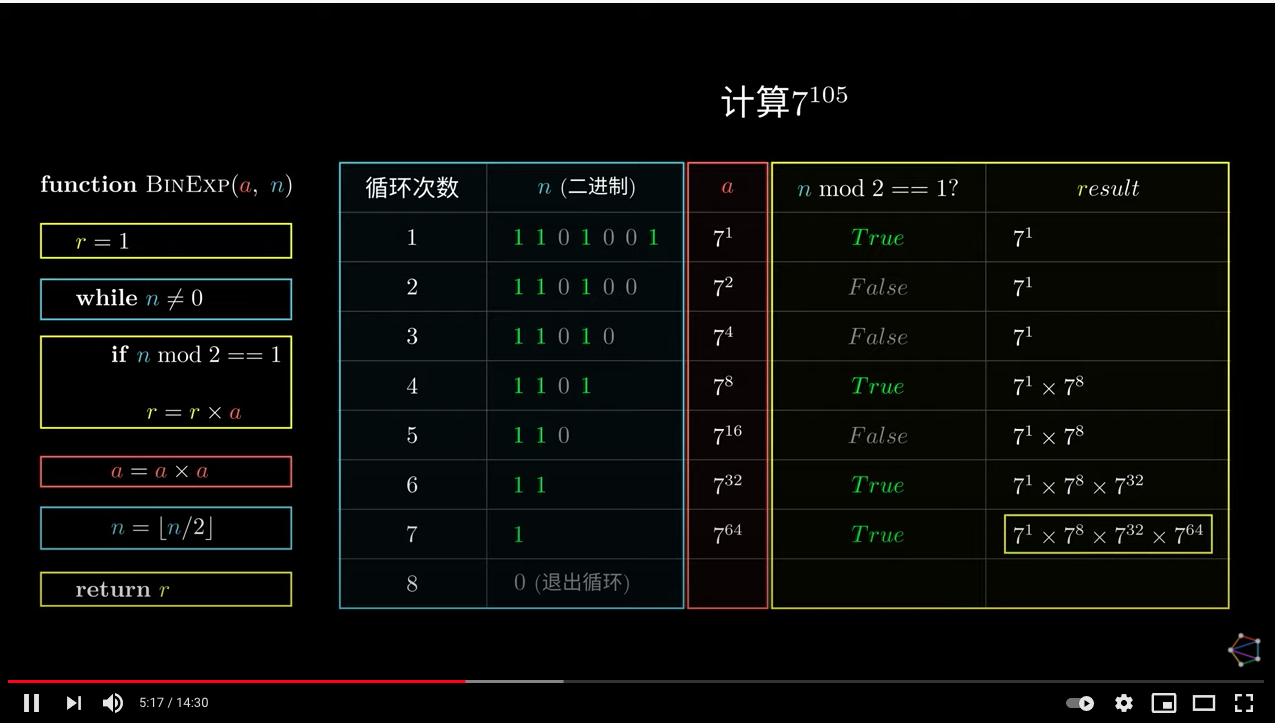
伪代码且以 $7^{105}$ 为例：

快速幂 JS 代码

$a^n$ mod m


function pow(a, n, m) {
  let usefulA = a % m
  let result = 1
  while (n) {
    if (n & 1) {
      result *= result % m
    }
    usefulA *= usefulA % m
    n >>>= 1; 
  }
  return result
}

快速幂 JS 代码

var countGoodNumbers = function (n) {
    const mod = BigInt((1e+9) + 7)
    const odd = Math.ceil(n / 2)
    const even = n / 2
    return pow(5, odd, mod) * pow(4, even, mod)
};