比特位计数

方法一：Brian Kernighan 算法

算法：对任何一个数 n，n & ( n − 1 ) 的结果是 n 的比特位最右端的 1 变为 0。

例如，n = 12 , n − 1 = 11 , 11 & 12 = 8

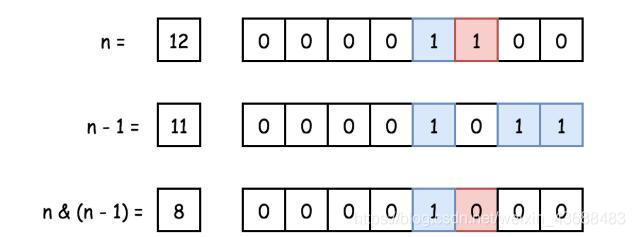
解释：结果 8 的 2 进制中，右边第三位为 1，因此经过「Brian Kernighan」计算变为了 0

因此只要重复计算对 n 进行重复计算, 直到 n 为 0，其中操作的次数，即为 1 的个数

伪代码：

while (n > 0)
  n = n & (n - 1)
  count ++

位运算：妙不可言！

最高有效位：对于正整数 x 而言，如果存在最大的正整数满足：

y <= x 并且 y 是 2 的整数次幂

则称 y 为 x 的最高有效位。

最高有效位的特性包括：

如何判断一个正整数是不是 2 的整数次幂，可以利用方法一提到的位与运算的性质，如果正整数 y 是 2的整数次幂，则 y 的二进制中只有最高位是 1，其余为 0.
因此当且仅当 y & (y - 1) = 0， y 为 2 的整数次幂

对于题目

看不懂 QAQ